Imagine for a moment that you’re a military officer serving in the Air Force. With a group of other officers, you want to make sure that your fighter planes are armored just the right amount and in the right places. Too much armor makes the planes slower and less maneuverable, whereas too little would make it easy for enemy combatants to shoot them down.
You start out with the first question: where should the armor go?
To find out which parts of the plane need the most protection, your team examines the planes that have come back from missions. You find out that the bullet holes aren’t uniformly distributed on the aircrafts; for example, there are about 50% more bullet holes per square feet on the fuselages than on the engines. That basically means that you can get the same amount of protection with less resources spent (or more protection with the same resources) if you focus on armoring the fuselage instead of the engines.

Then you move on to the other question. How much is the right amount?
Since that question requires more advanced math, you turn to the army’s math department. You don’t often see that department in the movies, as battles on the front line are much more dramatic and captivating than mathematicians, who fight the same wars with calculators and equations instead of bombs and machine guns. However, in real life they are just as important.
The answer that the real military officers in this situation got was probably not the one they expected. The math guru they asked for help told them that even the first answer they got was wrong: the armor should go to the parts with the least amount of bullet holes, not the most.
If you use exaggerated numbers, the picture becomes quite clear. Imagine that the planes that came back had zero bullet holes on the engines. What would that mean? Would it mean that the enemy fighters are as inaccurate as movie villains and never actually hit the good guys where it mattered? Or would it mean that if the planes got even a single shot to the engine casing they would fall down? The latter sounds quite a bit more plausible.
In the 2006 movie “Rocky Balboa” the name character gives a famous inspirational speech. If you haven’t seen it by now, just search “Rocky Balboa inspirational speech” on YouTube and you’ll find the clip. A part of what Rocky says is that “it’s not about how hard you’re hit, it’s about how hard you can get hit and keep moving forward. That’s how winning is done!”
Well, the planes that managed to return from battle were exactly the ones that got hit but were still able to keep moving forward. And as it turns out, it’s easier to keep moving forward if your aircraft gets hit in the fuselage than in the engine. But the officers who made the first assessment didn’t realize that there was a difference between the returning planes and the missing planes.
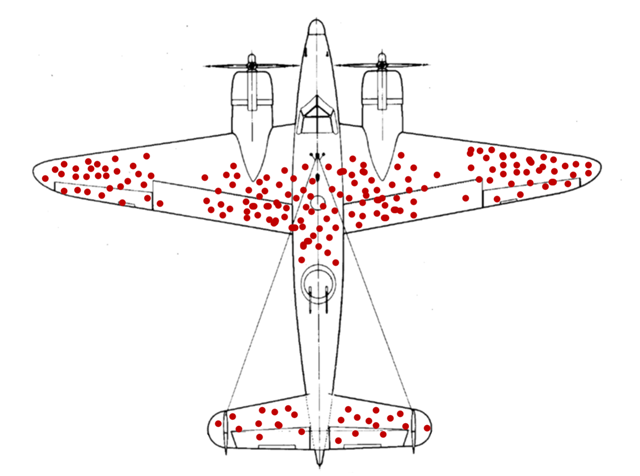
Image Copyright : Wikipedia
In scientific terms, this is called “Survivorship bias”. It’s the very human tendency to base your analysis on just the examples you see, without realizing that they must have “survived” something to get there.
To see another example of this in action, let’s take a glimpse at the world of finance. Many studies that evaluate the performance of mutual funds use either “end-of-sample conditioning” or “full-data conditioning”. The former means that you examine the track records of funds that exist at point of time X, while disregarding the ones that died before that point. The latter means examining funds that stay alive for the whole period of time from A to B, disregarding the funds that cease to exist between them. Mutual funds don’t live forever, and naturally the ones that vanish also tend to be the ones that perform the worst. Unsurprisingly, ignoring the worst cases leads to inflated performance statistics.

When choosing mutual funds to invest in, a lot of people tend to base their decisions on the performance histories. An investment bank might highlight its best performing fund on the front page and then a client looks at it and goes like “wow, it has had a steady 12% annual growth rate for the past ten years, the portfolio manager really knows what she’s doing, I’m definitely investing in this!”
But the truth is, if you start a bunch of funds, then some of them will fail and some of them will succeed. Then, if you look at only the survivors, you see “smart investment decisions” instead of blind luck.
Applications to Magic
The beauty of math is that the same principles can be used to solve many different types of problems in many different areas. By understanding concepts like the survivorship bias, you can recognize them when they occur and then make smarter decisions because of that.
Here are a couple of examples of how it can be applied to Magic. If you can think of some more, let me know in the comment section!
Story 1:
About a year ago, I was playing a Kaladesh Team Draft. My opponent was playing a Blue-Black deck that seemed to be splashing Red, and I had a black-white aggressive deck with Fabricate-creatures, 《Inspired Charge》 and some combat tricks. I had a pretty good start and curved out with some creatures, while my opponent played a turn 2 《Prophetic Prism》 and basically nothing else. He passed on turn 4 with something like two 《Island》, a 《Swamp》 and a 《Mountain》 up, and I had around three creatures in play. I attacked with the creatures, he took the damage and went down to a fairly low life total.
Now, I had two options: I could play another 3/3 creature, or hold up tricks in case he has an 《Incendiary Sabotage》, which I had seen in the draft and knew that my team mates didn’t have it in their decks. If I played around it, I could use my tricks to save two of my three creatures. One of my team mates had played against the same deck on the previous round and told that Red only seemed like a small splash and that the opponent’s own creatures were quite small, so it didn’t seem very likely that he would have it in his deck, as splashing for Double-Red cards is quite rough.
Furthermore, if I had been in his shoes, I would’ve cast the 《Sabotage》 during combat to avoid taking about 6 or 7 damage, especially as there is no guarantee that even if I play more creatures, they would be ones that die to the 《Sabotage》. Sooooo, I decided not to play around it, cast the creature in my hand and promptly got decimated by the sweeper.
There was one simple question that I forgot to ask myself: What could they have kept?
If your opponent keeps a seven card hand, it’s not just a random combination of seven cards. It’s a combination of seven cards that they decided were good enough to keep (or too lazy to send back). The hand had to “survive” the keep/mull process. They knew that I had an aggressive deck and that I was on the play. Would they keep a hand that only had a 《Prophetic Prism》 to cast before turn 5? No!
Or at least probably no. Let’s be real: sometimes people keep terrible hands. Or maybe they had like a 5 mana bomb in hand and hoped that being on the draw and having a 《Prophetic Prism》 would let them draw something to buy enough time to cast it. In that case, putting more pressure on by casting a creature could have been crucial.
But I was already quite far ahead so there was no reason to take the risk when I knew for sure that there was an 《Sabotage》 in the draft and that their team had it. Also, if he had a 《Sabotage》, he might have had a turn 3 or a turn 4 play as well, and just chosen to not cast them to get more value out of the sweeper.
Anyhow, the lesson here is that if your opponents draw looks a bit weird, ask yourself “What could they have kept?” and you might gain important insight into what they probably have.
Story 2:
I was playing the finals of a Magic Online Draft and my opponent had an evenly split three color deck that seemed quite weak. After easily defeating him in game 1, it was time to sideboard. And this time I managed to ask the right question: How did they get here?
Because it was the final round it meant that he had to have defeated two other players to come that far. He didn’t just have a random draft deck, he had “survived” the first two rounds. Pretty much all the cards he played in game 1 were mediocre at best with no real synergy, and his mana base seemed shaky, so I thought that the other half of his deck probably included some bombs.
Most of the time bad decks are a result of drafting colors or archetypes that aren’t open, and the most common reason for not being able to let go of a color is opening a bomb. His deck looked like a classic example of that.
So instead of sideboarding against the cards that I saw, I brought in a counterspell and a clunky but reliable removal spell in case he had something good. In game 2 he played 《The Scarab God》, I countered it and, uh… still lost. But even though I didn’t end up winning that game, the counterspell was very important because it gave me a chance. If I hadn’t been able to stop 《The God》, I would have just died immediately.
Now, drafts are only three rounds long. Have you ever done well on the day 1 of a Sealed GP? Those things are LONG, especially if you don’t have any byes. That means that at 7-0 your opponents’ decks are, on average, going to be much better than at something like 2-3. The deeper you go, the more the likelihood of your opponent having a good curve or some bombs increases. For example, you might want to save your 《Kefnet's Last Word》 a bit longer instead of using it on the first good target.
Story 3:
I’m quite sick of hearing comments like “Corey Burkhart went 4-1 against Ramunap Red with the UW Cycling deck at the GP, it seems like it should be a good matchup for Cycling.” If you listen to the stories of people who make the top 8 or the top 16 of a GP they all have great records against all other decks regardless of which deck they are playing themselves.
They have at most lost 2 matches during the weekend. Often those losses are to different decks, in which case they are X-1 at minimum against all matchups. One of the Ramunap Red players in the top 8 might have just as easily gone 5-0 against Cycling in the same tournament! Or rather: would have gone 5-0 if he had faced any, but didn’t because no one else at the top tables played Cycling because it’s just not a good deck compared to Temur and Red.
The trick is, once again, realizing that you don’t hear from the ones who lose. Except if they’re your friends. Then you probably hear from them a bit too much and have to listen to their bad beat stories on the car or plane ride back home.
I’m sure that while Corey did well, there was also a Cycling player who got stomped on by 《Rampaging Ferocidon》 and 《Bomat Courier》 because he was playing a deck with very little early interaction, bad removal spells and opponents who didn’t attack with all of their creatures into 《Settle the Wreckage》. I don’t know, maybe Corey’s opponents were like “Oh, he kept a seven card hand but hasn’t cast anything in the first four turns of the game. I should probably just press the advantage and not play around a sweeper!”
Thank you for reading!
Matti
P.S. For those who are interested, the original, better version of the story about the army mathematician and the bullet holes can be found in Jordan Ellenberg’s book “How Not to Be Wrong: The Power of Mathematical Thinking”.
Recommended Items
Share in Twitter
Share in Facebook
A Finnish player who won WMCQ and top 8’d in 2016 World Magic Cup as Finland representative.
Finished 28th in Pro Tour Aether Revolt, and missed narrowly one point shy of Gold level in 2016-17 season. Joins Hareruya Hopes in 2017-18 season and will play 2017 WMC as a team captain of Finland.















