Introduction

In Magic, as in other probabilistic domains, there are many questions that are easy to formalize but difficult to answer. A couple examples are how often a Tron player will have Tron in her opening hand, or how often you’ll hit your 4th land drop on time assuming you mulligan all 0 and 7-land hands. You could conceivably determine for the exact solution by pushing factorials around, but that’s painful to even think about.

One powerful statistical technique for answering these types of questions is Monte Carlo simulation. Monte Carlo simulation sounds fancy, but it essentially means just doing something over and over and tracking what happens. In the case of Magic, this would mean drawing thousands or millions of opening hands and counting how many of them have Tron. While doing this in real life would take weeks, even a cheap computer can solve a problem like this in seconds these days.

Monte Carlo simulation is how Frank Karsten got the numbers for his groundbreaking manabase articles (Part 1 / Part 2), and it’s how I got my first bit of notoriety in the Magic community. It’s also much easier to do than you’d expect. In this article, I’m going to walk you through a basic Monte Carlo simulation and introduce you to the basic techniques and guidelines. If you’re just interested in the practical Magic content, feel free to skip to the conclusion.

Problem Statement

The question we’re going to try to answer today is how often you’ll be able to cast the CCDD uncommons, ie. 《Nightveil Predator》 or 《Crackling Drake》, in “Guilds of Ravnica” limited. The hypergeometric distribution, the normal tool for answering this kind of question, doesn’t work here because we’re trying to track two different kinds of basic as well as dual lands.

How should we set the simulation up, then? Firstly, we should recognize that there are two different problems we can solve here. The first is how often we’ll have access to CCDD mana by turn 4 overall. The second is how often we’ll have CCDD mana given we’ve drawn 4 or more lands by turn 4. After all, it’s not fair to count getting stuck on lands in general against the CCDD cards. Any other 4-mana card would be similarly problematic.

After that, though, this is a straightforward situation where we want to draw a bunch of hands and see how often we get what we want.

Python

The programming language I’m going to be using is called Python. You can download it here. Python is completely free, and it’s my favorite programming language by a lot. It’s easy to learn, simple to read, and exceedingly elegant. There are a bunch of tutorials on the Python website to help you get started. I’m going to try to keep things simple enough that you’ll be able to follow along even if you don’t know anything about Python or programming in general, but it’ll help to be familiar with the basic concepts.

Importing Packages

Python comes with a bunch of useful packages pre-installed, but you have to tell it which ones you’re using so you can load them. ‘random’ is a package with tools for random operations, as you’d expect. ‘Counter’ is a tool for counting things. You can read the documentation on these packages here (random / Counter) if you’re interested in learning more.

Declaring Variables and Creating a Deck

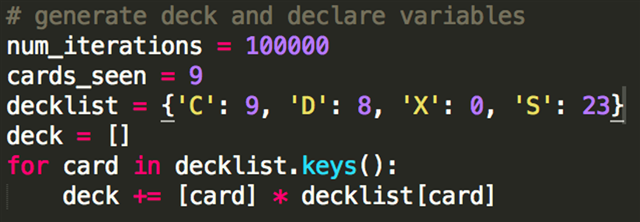
First of all, we need to tell the computer how long to simulate for and how many cards to look at in each simulation. We store these numbers as variables. This step isn’t strictly necessary, but it’s good practice to have these inputs at the beginning so it’s easy to locate and change them later if we want.

There’s no hard and fast rule for how many iterations to run, but a couple hundred thousand is usually good enough. If you run your simulation a couple times and get the same numbers each time, that’s a sign you’re doing enough iterations. I’m using a hundred thousand here mostly because it’s a nice round number.

For cards_seen, including your opening hand, you’ll have seen 10 cards by turn 4 on the play. Since we only care about whether we have CCDD mana if we’ve drawn the CCDD spell, we want to use 9. Note that we can change what turn we’re looking at or whether we’re on the play or the draw by increasing or decreasing this number.

Next, we need to make a virtual deck. We start by declaring a decklist as a dictionary. Dictionaries are one of Python’s two main data structures, and they’re typically bijective maps of strings to numbers. That is, you can use a dictionary to look a number up for a particular string. The order of the numbers and cards are reversed, but the decklist should look familiar.

To begin with, let’s consider a typical limited manabase with 9 basics of one color and 8 basics of another. We call one type of basic ‘C’ and the other type ‘D’. We’ll want to account for dual lands later, so we have an ‘X’ entry in our dictionary for duals even though we’re currently not playing any. Lastly, to fill out the deck, we need our 23 spells, or ‘S’. We don’t really care what the spells are, so we group them all together.

Next we need to generate a deck from our decklist. The for loop goes through every card in our deck and adds the corresponding number of that card to a list.

Simulation

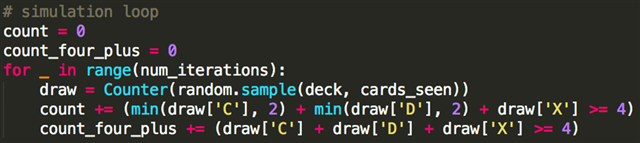
Now it’s time to simulate. We start by declaring two count variables. The first counts how often we have CCDD mana, and the second counts how often we draw 4 or more lands. It’s good practice to give these variables more detailed names than I have, but I’m personally pretty lazy about naming things.

Next, we have our for loop. ‘range’ is a Python function that takes an integer and gives you a list containing 0 through that integer, but not including it. Here, we’re using this list as an arbitrary object with a hundred thousand things in it. The underscore tells Python that we don’t really care about the numbers we’re iterating through. Overall, this line of code is the basic setup for doing the same thing a whole bunch of times in Python.

Now we need to tell Python what to do in each iteration. First, we’ll draw a hand of 9 cards and count how many types of cards are in it. ‘random.sample(deck, cards_seen)’ takes a random sample of ‘cards_seen’ cards from ‘deck’, ie. a hand and a couple draw steps. Feeding that sample into ‘Counter’ gives you a dictionary you can use to look up how many of each card were in the sample.

Then we need to figure out the minimum requirements to have CCDD mana. I’m doing some fancy things to get all of this in one line, but you could do the same operation with if statements as well. Essentially, to have CCDD mana, we need at least 2 C basics and at least 2 D basics, and dual lands can act as wild cards for either. This means we can count the first 2 of each kind of basic and all the dual lands, then check if we get 4 or more. When we do, we increment our count.

Similarly, we’ll increment ‘count_four_plus’ if the sum total of lands in our draw is 4 or greater.

Printing the Results

Lastly, we need to print the results. The details of this step aren’t important, but ‘print’ is a function that displays whatever you give it in the terminal. It’s the primary way of getting numbers inside your program out where you can see them.

We technically don’t care how often we draw 4 or more lands, but I like printing a number that I can easily verify as a safeguard against mistakes. In this case, we can check how often we draw 4 or more lands in our simulation against the number from a hypergeometric calculator.

Results

When we run our script, this is what we get:

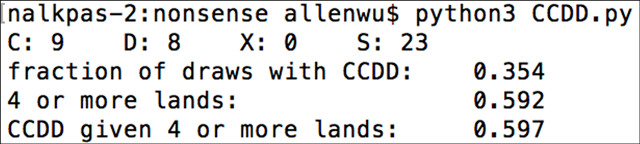
And that’s it. 26 lines of code.

Conclusion

All that’s left is to interpret our results. We can see that the numbers for the cookie-cutter limited manabase are pretty dismal. We’ll have the mana to cast our CCDD creature just 35.4% of the time, and even given we’ve drawn 4 lands, there’s still only a 59.7% chance we have the colors we need.

What happens if we add 2 dual lands to the mix, instead of 1 of each basic? Things look significantly better. We’ll have the mana we need 43.7% of the time, and we’re 73.6% to have the colors we need after we have 4 lands. We improve 8% overall against the cookie-cutter manabase and around 14% when we’ve draw enough lands. With 4 duals, we’ll have the mana we need around 50% of the time and we’re 83.9% to have the right colors when we have enough lands.

I should be clear that these numbers are a slight simplification. The probability we have the colors we need in 10 cards given we’ve drawn our CCDD card isn’t quite the probability we have CCDD mana in 9 cards. (Though we could remedy this particular problem by removing a spell from our decklist.) We’re also not accounting for the fact that our particular dual lands will always come into play tapped. I didn’t try to address these problems on purpose. Part of it is that I wanted to keep my code simple for didactic purposes, but it’s also important to recognize that we’re never going to account for everything. Even if we could, doing so probably wouldn’t be worth our time. But keeping the limitations of our models in mind, these numbers still serve as valuable guidelines.

For me, the clear takeaway from this experiment is that if I’ve drafted a CCDD card, I’m going to prioritize Guildgates much more highly. If I’ve drafted multiples, I’m going to go out of my way to get 4 Guildgates, even if I have to take them over solid playables for my deck.

Postscript

I have to say, I’m really not a fan of these CCDD designs. It’s absurd that a normal 2-color limited deck won’t be able to cast a 2-color spell over 40% of the time even if they’ve drawn enough lands for it. Not only that, these creatures are so impactful that the difference between casting one and having one rot in hand will completely decide a game of limited. I get that you don’t have to cast these spells on curve for them to meaningfully impact the game, but in my opinion they add too much instability and volatility to an already volatile game.

I felt the same way about the CCC designs in Dominaria. I like the theory that you can get these cards late in draft if you’re the only player in a particular color or guild, and they’re a real reward for finding the open lane in draft, but in practice these cards are also so powerful that it’s correct to speculate on them early. All in all, these cards are a big miss for me.

Anyway, hopefully this article has been helpful. You can find the full code for this article here.

If you have any thoughts or questions, please let me know on Twitter: @nalkpas.

Allen Wu