Translated by Takuma Kusuzawa

(編注 : 記事内の外部リンクは英語となっております。)

はじめに

マジックでは、他の確率が絡む問題でもそうですが、計算方法を考えるところまでは簡単でも、答えを計算するのが難しい問題がいくつもあります。いくつか例をあげると、トロンプレイヤーが初めの7枚でどれくらいトロンが揃うのか、とか、土地が0枚か7枚の手札はマリガンするとして、どれくらいの頻度で土地4枚を置き続けられるか、などがありますね。階乗なんかの計算をこねくり回せば正確な答えにはたどり着くでしょうけれど、そんなことを考えるのは辛すぎますよね。

こういった問題の結論を出すのに強力な統計の手法の一つに、モンテカルロ法というものがあります。モンテカルロ法なんていうとカッコイイ感じがしますが、本質的には、ただ何度も何度も繰り返して、結果を数えるだけなのです。マジックで言うと、初手を何万回、何億回と引き続けてみて、トロンが揃っていた回数をただ数える、ということです。これを自分の手で実際にやると何週間もかかりますが、今どきは安いコンピュータでも数秒で答えが出てしまいます。

モンテカルロ法はFrank Karstenがマナベースの記事 (Part 1 / Part 2) で数字を導き出したときに使った手法で、私がマジック界で少しばかり有名になったきっかけでもあります。あなたが思っているよりずっと簡単なものでもあります。この記事では、モンテカルロ法の基本的な考え方と実践の仕方について紹介します。マジックについての実用的な内容を期待していたようでしたら、結論まで飛ばしてしまってください。

問題提起

今日答えを出す問題は、『ラヴニカのギルド』リミテッドにおいて、CCDDアンコモン、例えば《夜帷の捕食者》や《弾けるドレイク》をどれくらい唱えられるか、です。このような問題を解くときに一般的に使われる超幾何分布では答えを出せません。基本土地と2色土地が問題を複雑にしているからです。

では、どのように計算を組み立てるべきでしょうか？まず、解かねばならない問題が2つあることを意識しないといけません。一つは、4ターン目にCCDDマナを出せるようになるのはそもそもどれくらいなのか。二つ目は、4ターン目までに4枚以上の土地を引いた上でどれだけCCDDマナが出せるか。CCDDカードについて言及する上で、そもそも土地が詰まった場合を含めるのはフェアじゃないですよね。他の4マナカードでも同じ問題があるわけですから。

ともかく整理が済んだことで、これはただたくさん引いてみれば結果がわかる問題だというのは分かりました。

Python

私が使うプログラム言語はPythonです。ここでダウンロードができますよ。Pythonは無料で使うことができ、色んな点で私の一番お気に入りの言語です。簡単に学べるし、シンプルで読みやすく、極めて上品なんです。使い始めるにあたって、Pythonのウェブサイトに大量のチュートリアルがあります。Pythonやプログラムのことを知らなくて分かりやすいように、できるだけシンプルにしようと思っていますが、このチュートリアルは基本的な概念を理解するための手助けにもなりますよ。

パッケージのインポート

Pythonにはたくさんの便利なバッケージがインストールされている状態で付いてくるのですが、どれを使うか明示しないといけません。「random」は文字通り、ランダムな処理をさせるためのツールです。「Counter」は色々なものを数えるときに使います。詳しく勉強したい場合には、それぞれの説明をこちらで見ることができます。 (random / Counter)

変数を宣言して、デッキを作ってみる

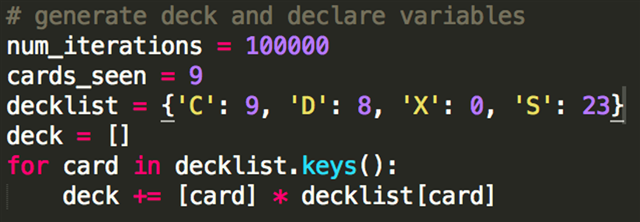
まずはじめに、コンピュータに対して、どれくらいの回数試すのか、各試行で何枚のカードが入っているかを伝えないといけません。こういった数は変数として収めておきます。この手順は厳密には必要ないのですが、始めはこうしておくことで簡単に指示ができるようになるので、いい練習になりますし、あとで変えることもできます。

何回反復させるかは、特に難しいルールはないのですが、数十万回あたりで大体十分です。何回かシミュレーションを動かしてみて同じ結果を毎回得られたなら、十分な回数だという印ですね。しっくりくる感じがするので、私は大体十万回にしています。

「cards_seen」が意味しているのは、初手を含めて先手の4ターン目に10枚のカードを引くということです。CCDD呪文をキャストするときにCCDDマナが出せるかを見たいので、このCCDD呪文を引いた9枚で検討しないといけないというわけですね。何ターン目での可能性を見るか、また先手後手それぞれの検証は、ここの数字を増減させることで調整できることを覚えておきましょう。

続いて、仮のデッキを作りましょう。まず、「decklist」をdictionaryとして定義します。dictionaryはPythonの主なデータ構造二つのうちの一つで、文字列と数値の全単射の羅列で構成されます。要は、特定の文字列に対応した数字を探しだすための「辞書」なのです。数字とカードの順番が逆ですが、デッキリストに似て見えると思います。

始めるにあたって、リミテッドのマナベースを一色目が9枚、2色目が8枚としましょう。片方をC、もう片方をDと呼ぶことにします。2色土地も数えたいと思いますがこれは一度おいておきましょう。今は1枚も入れませんが、Xという文字を後の2色土地のために設定しましょう。最後に、デッキを埋めるためには23枚の呪文が必要ですね、これをSとします。呪文が具体的に何かは気にしないので、一緒にしてしまいましょう。

そしてデッキリストからデッキを生成します。forループがデッキに入るカード1枚1枚に通し番号を付けていきます。

シミュレーション

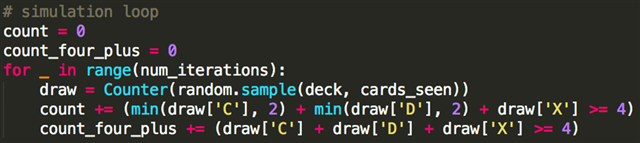
さぁ、実践の時間です。二つの数字を数える変数を宣言します。一つはどれだけCCDDマナが揃うか、もう一つは4枚以上土地があるか、です。この変数にもう少し具体的な名前をつけると教科書として良くなるのですが、私は名前をつけるのをめんどくさがりがちなのです。

続いて、forループを作ります。「range」はPython関数で整数を入力すると、0から入力された数までの整数のリストを返します。ここではこのリストを十万個の物が並べられるオブジェクトとして使います。アンダースコアは、各数値自体には意味がないとPythonに伝えています。全体でみると、この一行はPython上で同じことを大量に繰り返すための準備なのです。

さて、次はPythonに一度の処理で何をするか伝えないといけないですね。まず、9枚の手札を引き、種類ごとにカードの枚数を数えます。「random.sample (deck, cards_seen)」は「deck」からランダムで選び「cards_seen」に加えます。これは手札とドローを表現しています。この選ばれた結果を「Counter」に通すことで、引いたサンプルに各種類のカードが何枚あるか数えられるdictionaryを得られるわけです。

続いて、CCDDマナを満たす条件というのを決めないといけません。一行で結果を得るために小洒落たことをしていますが、if分岐でも同じ処理ができます。CCDDマナを得るためには、本質的にはC土地2枚とD土地2枚が必要で、2色土地はワイルドカードとして働きます。つまり、各基本土地ごとに始めの2枚までと2色土地全部を数えていき、その合計が4枚以上になればよいのです。もしそうなったら、「count」を1増やします。

同様に、土地の合計が4以上になれば「count_four_plus」を増やしていきます。

結果の出力

最後に、結果を表示させないといけませんね。この部分に関しては細かいことを気にしなくてもいいですが、「print」は指定したものをターミナル画面に表示させるものです。プログラムの中から数字を私達に見える形で表示させる代表的な方法です。

土地が4枚以上引ける割合は気にしませんが、プログラムが間違っているか簡単に分かるように、確認手段として必要ない数字もよく表示させます。今回は、土地が4枚以上の割合を超幾何計算での数字と比較することで確認できます。

結果

スクリプトを走らせて出てきた数字がこちらです。

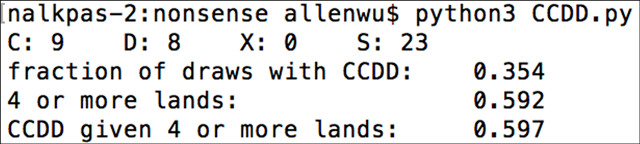
これでおしまい。たった26行のコードです。

結論

残るは結果を分析するだけです。大量に計算した結果の数字は残念なものだと分かります。CCDDクリーチャーを唱えられるマナを得られるのは35.4％しかなく、土地がそもそも足りなかった場合を除いても59.7%でしか必要な組み合わせを得られません。

基本土地1枚ずつを2色土地2枚に変えたときにどうなるか。結果は劇的に改善するようです。43.7％で唱えられるようになり、土地の枚数が揃いさえすれば73.6%で色の組み合わせも満たされることが分かりました。総合的に8%の改善、土地が引けた場合のみを考えると14%も向上しました。4枚の2色土地になると大体50%で唱えられ、土地の枚数が足りれば83.9%で色も揃います。

ここで明確にしておかないといけないのは、少し計算を簡単にしていることです。10枚でCCDDカードを引きつつ土地が揃っている確率は、9枚でCCDDマナが出せる確率とは異なります (この問題に関しては、デッキリストから1枚呪文を削ってやると解決できますが)。また2色土地がタップ状態でプレイされることも加味していません。この問題はわざと気にしないようにしました。その理由の一つは、コードを分かりやすくするためにシンプルにしたかったからなのですが、全てを考慮しての計算はできないということを意識することも重要です。仮にもしできたとしても、時間をかけるほどの価値はおそらくないと思います。それよりも限定的な条件であると意識して考えられれば、出てきた数字は指標として十分に活用できるはずです。

私にとって、この実験から得られた明確な事実は、CCDDカードをピックできたなら、ギルド門の優先度を思っていたより大きく上げないといけないということです。複数枚ピックしたなら、堅実なプレイアブルカードを流してでもギルド門4枚を確保するでしょう。

終わりに

実際のところ、私はCCDDサイクルが好きというわけではないと言っておかねばなりません。リミテッドでの平均的な2色デッキでは、土地が足りていても40%でしか2色のカードを唱えられず、現実的ではありません。このクリーチャーたちは強力なので、唱えられるのと手札で抱えるのとではゲームを左右しかねません。より効果的にゲームを動かすため、カーブに沿って4ターン目に唱える必要もないのですが、私としては不安定さが大きすぎるだけでなく、ただでさえ状況の変わりやすいゲームがより複雑になります。

『ドミナリア』のCCCサイクルでも同じことを感じました。このカード郡は同じ色やギルドのプレイヤーがいなければ遅い順目でも手に入る、という理論は好きで、ドラフトで空いてる枠を見つけられたときのご褒美だと思っていました。しかしながら、練習においてこれらのカードは強すぎたため、早い順目でピックを検討をするのが正しいように感じていたのです。とはいえ、最終的な結論としてはそもそもピックすること自体が大きな間違いだったようですね。

ともかく、この記事がみなさんの役に立てたらいいなと思っています。この記事で出てきたソースコード全文はこちらにおいてあります。

何か思うことや質問があれば、ぜひツイッターでお知らせください : @nalkpas。

アレン・ウー